Ever seen a manual clock in your home or elsewhere? Yes? Great! You may have noticed that it has two hands on its face — one that indicates the hour and the other showing the minute. Notice the point (at the center) at which both the hands meet, forming a cone-like shape.
Except for the time when the two hands are on top of each other (12 o’clock or 6.30), they are always separated, forming what is known as an angle in geometry at their meeting point. In other words, an angle is formed when two lines meet at the same point.
What are the various parts of an angle?
How is an angle calculated?
What are the different types of angles?
You must be having plenty of such questions. So, let us delve right into answering them.
What is an angle in geometry?
In geometry, an angle is formed when two lines or rays join at the same endpoint, also known as the vertex. An angle is always represented using the symbol ∠. Here is an illustration.
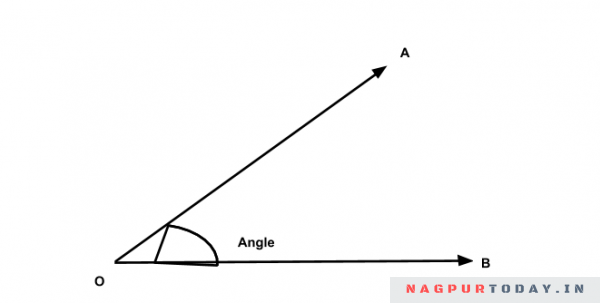
For example, in the above figure, O is the vertex, while A and B are the two rays that are forming the angle. The angle here is denoted as ∠AOB, and the two rays or arms for this angle are OA and OB.
How do you normally label an angle? Well, for this example, ∠AOB is the label used to define the angle – or you can simply label it in short as “O” (being the vertex). Other common forms of angle labelling used in geometry include Greek alphabets like α (alpha) or θ (theta).
How is an angle calculated? Let us look at that next.
How is an angle calculated?
First, let us go back to our clock example. If the minute hand comes close to the hour hand, the angle between the two hands becomes less, isn’t it? In fact, if the two hands are on top of each other (for example, at 12 o’clock or 6.30), the angle would almost be zero.
On the other hand, if you take the minute hand away from the hour hand, the angle will increase. For example, at 6 o’clock, the angle would be equal to half of the clock face.
In other words, the closer the two rays forming an angle are, the smaller the angle – and the further away the two rays are from each other, the larger the angle.
How is an angle calculated? We know that a full circle is calculated at 360O (or 360 degrees). Similarly, a half circle rotation would be 180O while a quarter circle would be 90o. An angle is also calculated on the same principle and using degrees. If you were to divide the entire circle into multiple parts (imagine a pizza!), the sum of all the angles in the circle would be 360o.
Here are a few examples:
- If the two arms are placed in a half circle position (for example, 6 o’clock or 9.15), the angle is calculated as 180o.
- If the two arms are placed in a quarter circle position (for example, 9 o’clock or 3 o’clock), the angle is calculated as 90o.
- If the arms are placed anywhere within the quarter circle position (for example, 3.10 or 8.55), the calculated angle would be between zero to 90 degrees.
- If the arms are placed in between the quarter circle and half circle positions (for example, between 9 o’clock and 9.15), the angle could be anywhere between 90 and 180 degrees.
- If one of the arms is now stretched beyond the 180-degree position, the angle would be calculated anywhere above 180O up to 270o.
Note: The sum of all the angles within a circle is always 360o while all the angles within a triangle always add up to 180o.
To measure an angle accurately, you need to use a measuring instrument called a protractor.
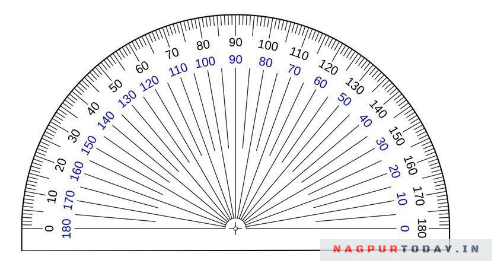
Protractors are extensively used to measure from zero to 180 degrees and can measure your angle accurately to the last degree. A protractor represents a half circle and is sufficient to measure most angles.
Which are the different types of angles that are used in geometry? Let us discuss them next.
Types of Angles
Primarily, these are the types of angles used in geometry:
As seen, an acute angle is the smallest angle with a measurement of less than 90 degrees, while the complete angle is the largest angle with a measurement of 360 degrees.
Additional Types of Angles
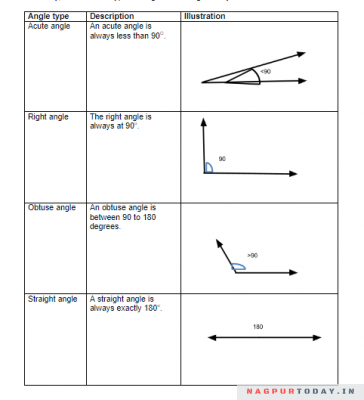
In addition to these six types of angles, you also have interior and exterior angles.
For example, look at the following figure.
Interior angles are all the angles within the shape (in this case, the triangle). Thus, ∠ABC ∠ BAC, and ∠ACB are all interior angles.
Exterior angles are those that are outside the shape – for the above example, ∠ACD is the external angle.
Also, note that in the above example, if you add ∠ACB to ∠ACD, the sum will be 180o – no matter what each of the angle measurements are. This is what is called as supplementary angles, or angles that always add up to 180o. In other words, angles on either side of a straight line (in this case, B-C-D) will always be supplementary angles. For example, if one of them is an acute angle (say, 50o), the other one will always be 180-50 (or 130O). On the same note, if the straight line is broken up into 4 angles, with three of them measuring 40O, 50o, and 60o, the last angle will measure:
180-(40+50+60) that is equal to 30o
A complementary angle is two (or more) angles that always add up to 90o – like that of a right angle. Example, in the above figure, ∠BAC and ∠ACB add up to form a complementary angle, as their sum will always be 90o. This is because the triangle (shown in the illustration) is a right-angled triangle, as it contains one right angle, namely ∠ABC. As we have learned that all angles within a triangle add up to 180o, the two acute angles in the depicted triangle would always add up to 90o – thus making them complementary.
Fun fact: Take any complementary (or supplementary) set of two angles. If you try to increase (or decrease) one of the angles in the set, the other one automatically decreases (or increases) such that their total measurement would always remain 90o or 180o.
Traversal Line and Angles
Parallel lines can never form an angle as they never meet. However, consider a traversal line that crosses two (or more) parallel lines. Here is an illustration where the blue-coloured traversal line is intercepting the 2 parallel lines at points A and B.
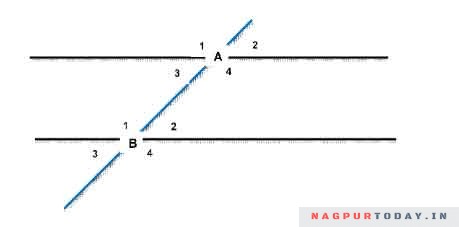
As seen, there are four sets of angles that are formed at each of the interception points A and B. These are all pairs of angles that have special properties as listed below:
- The sum of all the angles at the same interception point (for example, A1, A2, A3, and A4) will always be 360o.
- Vertically opposite (or vertical) angles (example, A1 and A4) will always be the same value.
- Corresponding angles at the two points (example, A4-B4 or A3-B3) will also have the same value.
- Consecutive interior angles (example, A3-B! and A4-B2) will always add up to 180o. Similarly, alternate interior angles (for example, A3-B2 and A4-B1) will always have the same value.
- Alternate exterior angles (for example, A1-B4 and A2-B3) will always have the same value.
Can you also observe the supplementary angles in the above figure? Yes, there are quite a few of them, including A1-A2, A1-A3, B3-B4, B2-B4, and more.
To summarise, angles make it so much more fun to learn geometry. Not just in geometry, you can observe angles in so many real-life objects around you, like the pointed roof of your house, a cone-shaped hat, scissors, or even your clothes hanger or chair. As outlined in this article, we have so many different types of angles that are formed when used with other geometrical shapes like triangles, straight lines, and even parallel lines.
Can you try sharing some examples of where you have seen a right angle or any other angle types in real-life objects around you? We look forward to reading your comments. So, keep posting.
Reference links:
https://www.mathsisfun.com/angles.html
https://www.splashlearn.com/math-vocabulary/geometry/angle






















